https://www.acmicpc.net/problem/1389
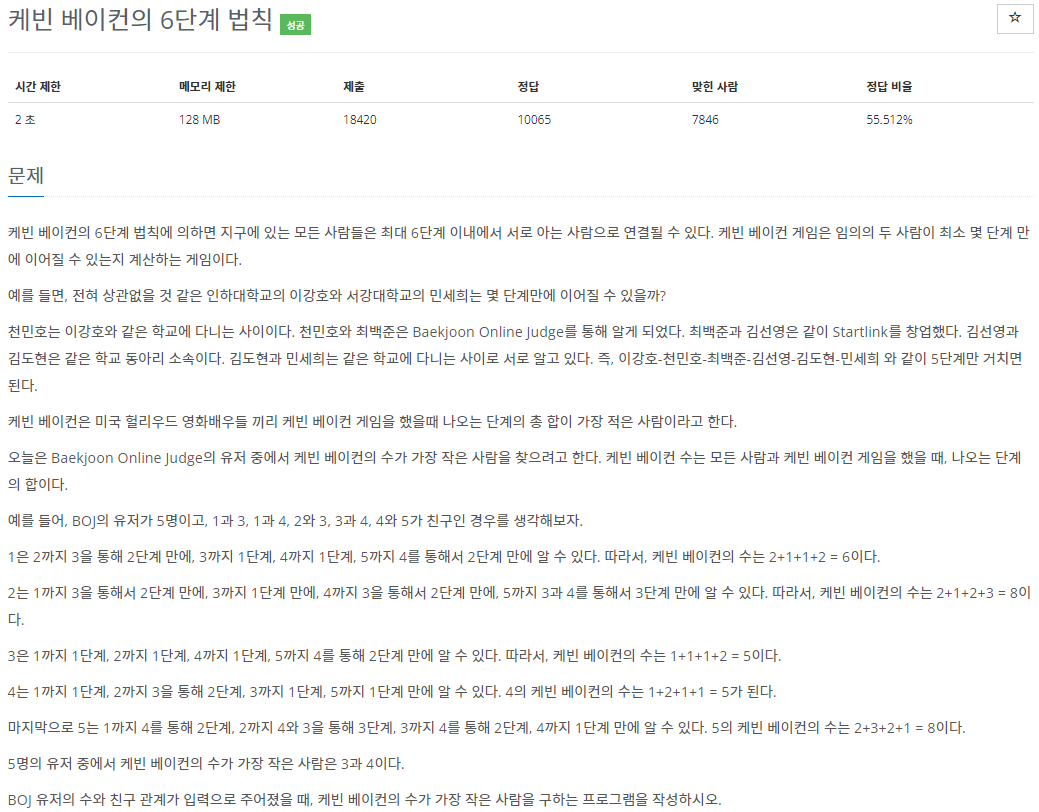
1389번: 케빈 베이컨의 6단계 법칙
첫째 줄에 유저의 수 N (2 ≤ N ≤ 100)과 친구 관계의 수 M (1 ≤ M ≤ 5,000)이 주어진다. 둘째 줄부터 M개의 줄에는 친구 관계가 주어진다. 친구 관계는 A와 B로 이루어져 있으며, A와 B가 친구라는 뜻
www.acmicpc.net
1. 접근

먼저 최대값과 시간 복잡도를 구해보자면 모든 관계를 다 둘러보아도 5,000번이면 되니 최대값은 넉넉하고 시간 복잡도로는 유저(간선)마다 각각의 케빈 베이컨 수를 구해야 하니 (유저 수 + 관계) * 유저수 = 100,000로 시간 또한 넉넉하다.
문제의 설명을 그래프와 표로 정리하자면 다음과 같다.
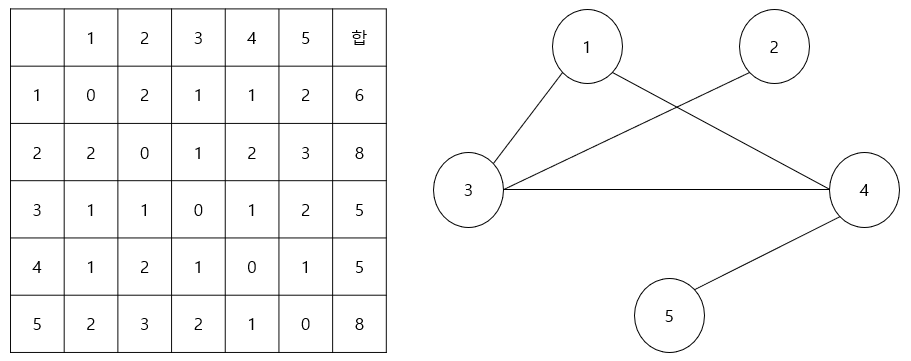
표와 같이 각 유저의 케빈 베이컨의 수를 구해주고 최소값을 가지고 있는 최소 인덱스를 출력해주면 된다!
2. 접근
전역 변수 및 input
static int N, M;
static ArrayList<Integer>[] graph;
static int[] dist;
public static void main(String[] args) throws IOException {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); // 친구의 수(V)
M = Integer.parseInt(st.nextToken()); // 관계의 수(E)
dist = new int[N + 1]; // 카운트 체크
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 1; i <= M; i++) {
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken()), y = Integer.parseInt(st.nextToken());
graph[x].add(y); // x번 유저와 y번 유저는 연결되어 있다!
graph[y].add(x); // 무방향 그래프로 반대 입장도 연결하자!
}
solution();
}
BFS 호출 및 최소값 비교
// N만큼 각각 BFS를 돌려 최댓값을 갱신한다.
static void solution() {
int minCnt = Integer.MAX_VALUE, minIdx = 0; // 최소 카운트와 해당 정점 번호
for (int i = 1; i <= N; i++) {
int cnt = BFS(i);
if (minCnt > cnt) { // 최소 카운트 및 정점 번호 갱신
minCnt = cnt;
minIdx = i;
}
}
System.out.println(minIdx);
}
BFS
static int BFS(int start) {
Arrays.fill(dist, -1); // 방문여부 및 카운트 초기화
int cnt = 0;
Queue<Integer> Q = new LinkedList<>();
Q.add(start);
dist[start] = 0;
while(!Q.isEmpty()) {
int x = Q.poll();
for (int y : graph[x]) {
if (dist[y] != -1) continue;
dist[y] = dist[x] + 1;
cnt+= dist[y]; // 이동 횟수를 누적해주자!
Q.add(y);
}
}
return cnt;
}
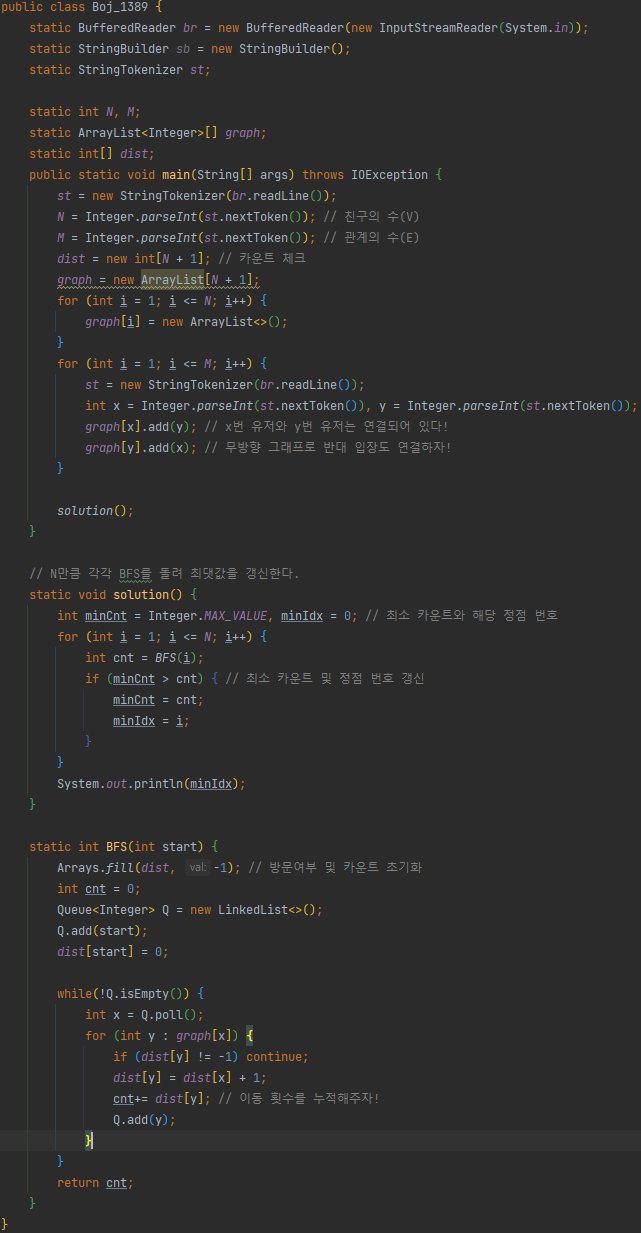
3. 전체코드
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 3055 탈출 JAVA (0) | 2021.12.09 |
|---|---|
| 백준 5567 결혼식 JAVA (0) | 2021.12.09 |
| 백준 1697 숨바꼭질 JAVA (0) | 2021.12.08 |
| 백준 18404 현명한 나이트 JAVA (0) | 2021.12.07 |
| 백준 2644 촌수계산 JAVA (0) | 2021.12.07 |