1. 알고리즘이란?
이론적으로 컴퓨터를 사용한 문제 해결의 가능성이라는 측면에서 0개 이상의 입력과 1개 이상의 출력이 있어야 한다, 각 명령은 단순 명확해야 한다, 한정된 수의 단계를 거친 후 종료되어야만 한다, 모든 명령은 컴퓨터에서 실행 가능해야 한다.로 총 네 가지의 조건을 만족해야 한다. 하나의 문장으로 종합하자면 주어진 문제의 대한 해답으로 모호함 없이 간단하며 컴퓨터가 수행 가능한 유한개의 명령을 순서에 따라 구성한 것이다. 다만 컴퓨터로 해결할 수 있어도 처리 과정이 너무 오래 걸려 현실적으로 해결할 수 없는 문제도 있기에 효율성 또한 충분히 고려되어야 할 조건이다.
2. 자료구조와의 연관성
효율적인 프로그램을 위해서는 효율적인 알고리즘이 필요하며 효율적인 알고리즘을 위해 적합한 자료구조를 선택해야 한다. 같은 결과를 처리하는 프로그램을 만들더라도 어떤 자료구조를 기반으로 데이터를 처리하고 조작하여 표현 했는지에 따라 그 성능은 천차만별이다. 흔히 알려진 게임인 UP & DOWN 게임을 예로 들어보자. 1 ~ 100의 범위 안에서 임의의 숫자가 하나 있다고 가정했을 때 가장 단순한 방법은 앞에서, 혹은 뒤에서부터 하나씩 확인해보는 방법이지만 최악의 경우 100번 확인해야 정답이 나올 수 있다. 하지만 오름차순으로 정렬되어 있다고 가정했을 때 중간값을 선택해 나가며 최대 7번이면 정답을 찾아낼 수 있다.

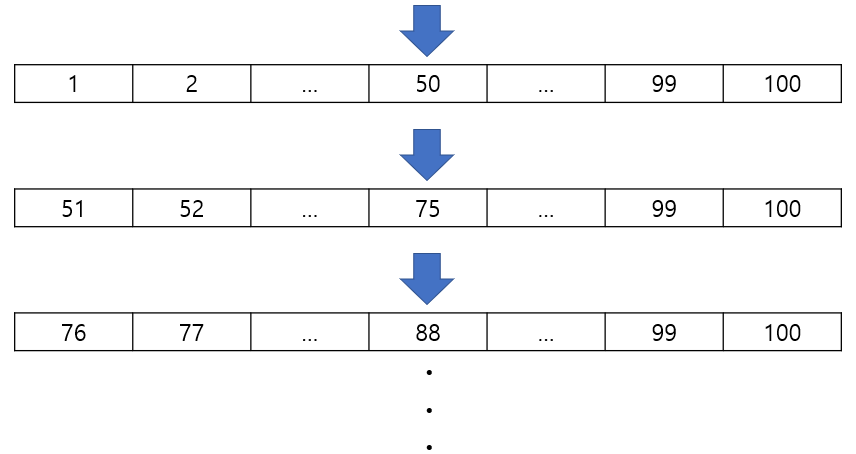
이처럼 주어진 문제와 조건들이 다양하여 한 가지 알고리즘으로 모든 방법에 효율적인으로 동작시킬 수는 없다. 따라서 주어진 문제나 조건들을 파악하여 각각 그에 맞는 자료구조를 선택하여 설계할 수밖에 없다.
3. 대표적인 알고리즘
일반적으로 잘 알려져있고 많이 사용되는 알고리즘은 분할 정복, 동적 프로그래밍, 욕심쟁이 방법이 있다. 분할 정복 방법은 주어진 하나의 문제를 작은 단위로 분할하여 문제를 해결하고 해결된 작은 단위의 문제를 결합하여 원래 문제의 답을 얻어내는 방법이다. 동적 프로그래밍 방법은 하나의 문제를 작은 문제로 쪼갠다는 관점에서 분할 정복과 비슷하다 볼 수 있지만 분할 정복에서는 쪼개진 문제들은 모두 독립적이지만 동적 프로그래밍에서의 문제들은 그 결과를 쌓아가며 답을 도출해 내기 때문에 독립적이지 않아도 된다. 마지막으로 욕심쟁이 방법은 전, 후 상태는 고려하지 않고 매 선택마다 최선의 선택을 해 나가는 것이며 매 선택의 최선 == 총결과의 최선일 수도 있다 라는 가정하에 풀어나가는 방법이다.
4. 알고리즘의 분석
정확하고 효율적인 알고리즘이라면 유효한 입력이 주어졌을때 유효한 시간, 유효한 자원 안에서 정답을 도출해내야 한다. 이에 대한 계산으로 공간 복잡도와 시간 복잡도 두 가지를 계산하여 사용하게 되는데 공간 복잡도는 해당 문제를 풀기 위해 필요한 총메모리의 양을 의미한다. 시간 복잡도의 경우 프로그래밍 언어나 연산을 수행하는 컴퓨터의 속도 등 여러 가지 요소에 영향을 받지 않아야 공통적인 데이터를 도출해낼 수 있으므로 최악의 데이터가 들어왔을 때 몇 번의 연산을 하고 얼마나 걸리는가? 를 시간 복잡도의 척도로 잡고 있다. 이 시간 복잡도를 나타내기 위해서는 점근 성능을 알아야 하는데 간단하게 설명하자면 입력 크기 n에 따라 결정되는 성능을 뜻한다. 최상의 시간 복잡도인 Big-omega와 평균적인 시간 복잡도인 Big-theta가 있지만 가장 많이 쓰이는 최악의 상황을 가정한 Big-oh 표기를 많이 쓰고 있다. 이는 계산식 내에서 결괏값에 가장 큰 영향을 끼치는 최고차 항만을 이용하여 표시한다.
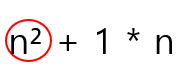
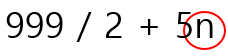
주어진 입력 n에 따른 표기법은 대부분 다음과 같다.
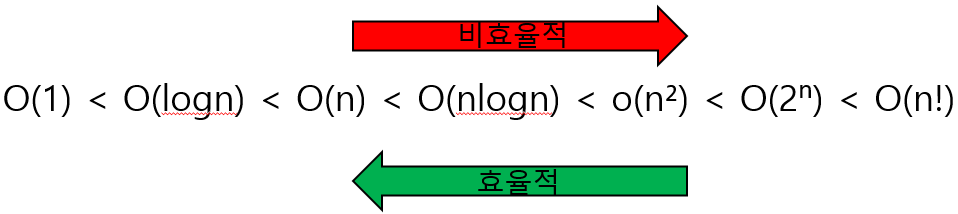
이어서 대표 알고리즘을 이용한 정렬 알고리즘, 탐색 알고리즘에 대해 알아보자!