https://www.acmicpc.net/problem/7569
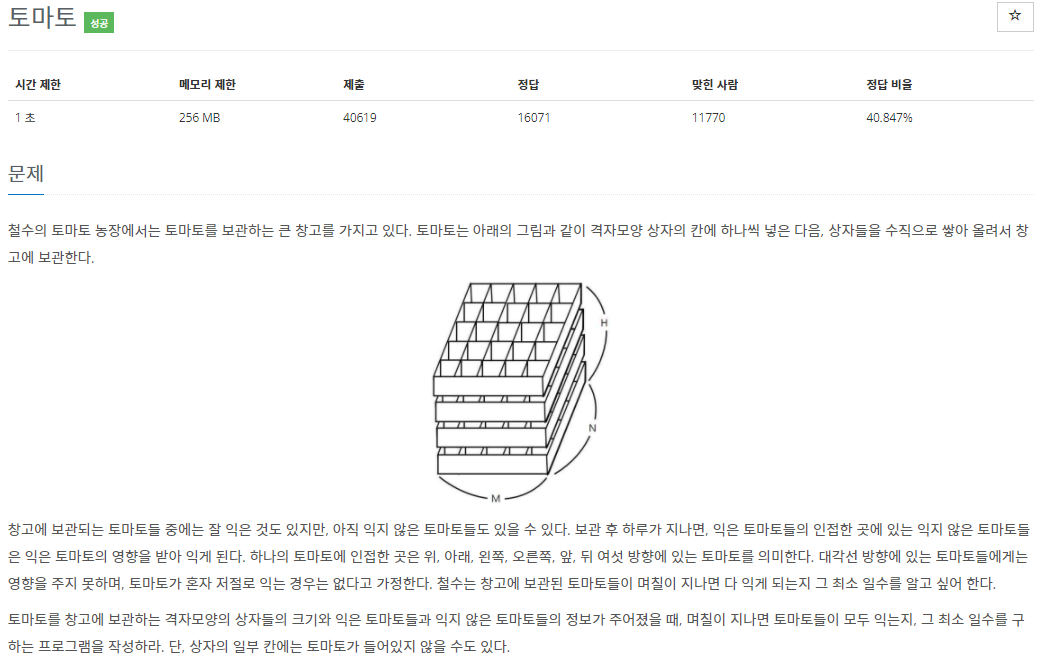
7569번: 토마토
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100,
www.acmicpc.net
1. 접근
최대 입력값에 따른 시간 복잡도는 다음과 같다.

칸의 갯수 = H * N * M = 1,000,000로 시간제한안에 여유있게 풀 수있다!
문제의 조건을 살펴보자

익은 토마토 기준으로 상,하,위,아래,좌,우 총 여섯 방향으로 토마토는 익어가며 토마토가 비어있는 칸도 있다.
첫 번째 입력 예제를 그림으로 보면 토마토가 잘 익어가다가 비어있는 칸으로 인해 모두 익지 못하는 경우가 발생한다.

두 번째 입력 예제는 판은 하나 늘어났으나 사방을 가로막는 비어있는 토마토가 없기에 모두 익을 수 있다.
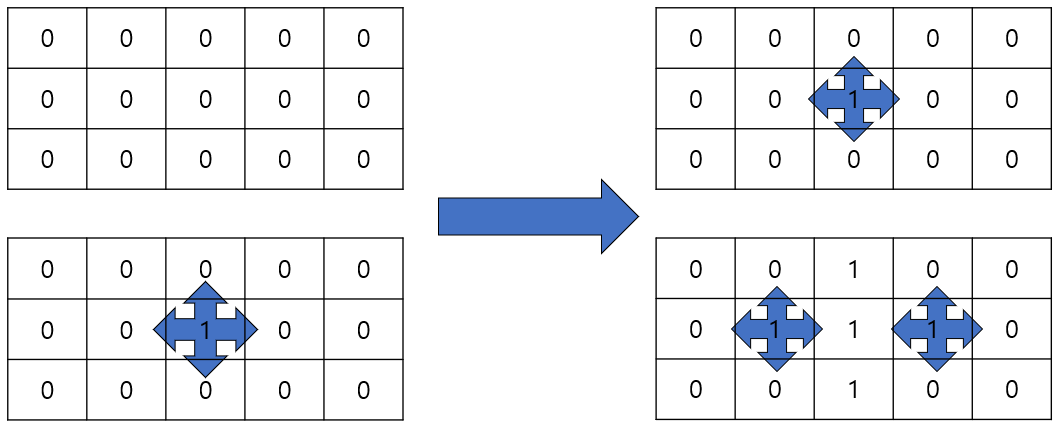
높이가 주어지기에 상, 하에 관한 좌표만 추가하면 기존에 최단거리를 찾는 멀티 BFS를 그대로 사용할 수 있다.
static int[][] dir = {{-1, 0, 0}, {0, 1, 0}, {1, 0, 0}, {0, -1, 0}, {0, 0, 1}, {0, 0, -1}}; // N, M, H
다음 좌표를 하나하나 찾아가며 토마토를 익혀나간 후 BFS가 끝나면 방문하지 못한 칸이 있는지 확인 후 출력하면 된다.
2. 풀이
변수 세팅
static int N, M, H;
static int[][][] A, dist;
static int[][] dir = {{-1, 0, 0}, {0, 1, 0}, {1, 0, 0}, {0, -1, 0}, {0, 0, 1}, {0, 0, -1}}; // N, M, H
public static void main(String[] args) throws IOException {
st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
dist = new int[H][N][M];
A = new int[H][N][M];
for (int i = 0; i < H; i++) {
for (int j = 0; j < N; j++) {
st = new StringTokenizer(br.readLine());
for (int k = 0; k < M; k++) {
A[i][j][k] = Integer.parseInt(st.nextToken());
}
}
}
solution();
}
배열 초기화 및 정답 출력
static void solution() {
for (int i = 0; i < H; i++) {
for (int j = 0; j < N; j++) {
Arrays.fill(dist[i][j], -1);
}
}
BFS();
int answer = 0;
for (int i = 0; i < H; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < M; k++) {
if (A[i][j][k] == -1) continue; // 벽은 원래 방문하지 못한다.
if (dist[i][j][k] == -1) { // 방문하지 못한 칸이 있다 == 다 익지 못한다.
answer = -1;
System.out.println(answer);
return;
}
answer = Math.max(answer, dist[i][j][k]); // 구해진 최단거리중 제일 큰 값 갱신
}
}
}
System.out.println(answer);
}
BFS
static void BFS() {
Queue<Integer> Q = new LinkedList<>();
// 토마토의 위치를 담는다.
for (int i = 0; i < H; i++) {
for (int j = 0; j < N; j++) {
for (int k = 0; k < M; k++) {
if (A[i][j][k] == 1) {
Q.add(i);
Q.add(j);
Q.add(k);
dist[i][j][k] = 0;
}
}
}
}
while(!Q.isEmpty()) {
int z = Q.poll(), x = Q.poll(), y = Q.poll();
for (int i = 0; i < 6; i++) {
int nx = x + dir[i][0];
int ny = y + dir[i][1];
int nz = z + dir[i][2];
if (nx < 0 || ny < 0 || nz < 0 || nx >= N || ny >= M || nz >= H) continue; // 배열범위 초과
if (dist[nz][nx][ny] != -1) continue; // 이미 방문
if (A[nz][nx][ny] != 0) continue; // 토마토가 없거나 이미 익은 토마토임
dist[nz][nx][ny] = dist[z][x][y] + 1;
Q.add(nz);
Q.add(nx);
Q.add(ny);
}
}
}
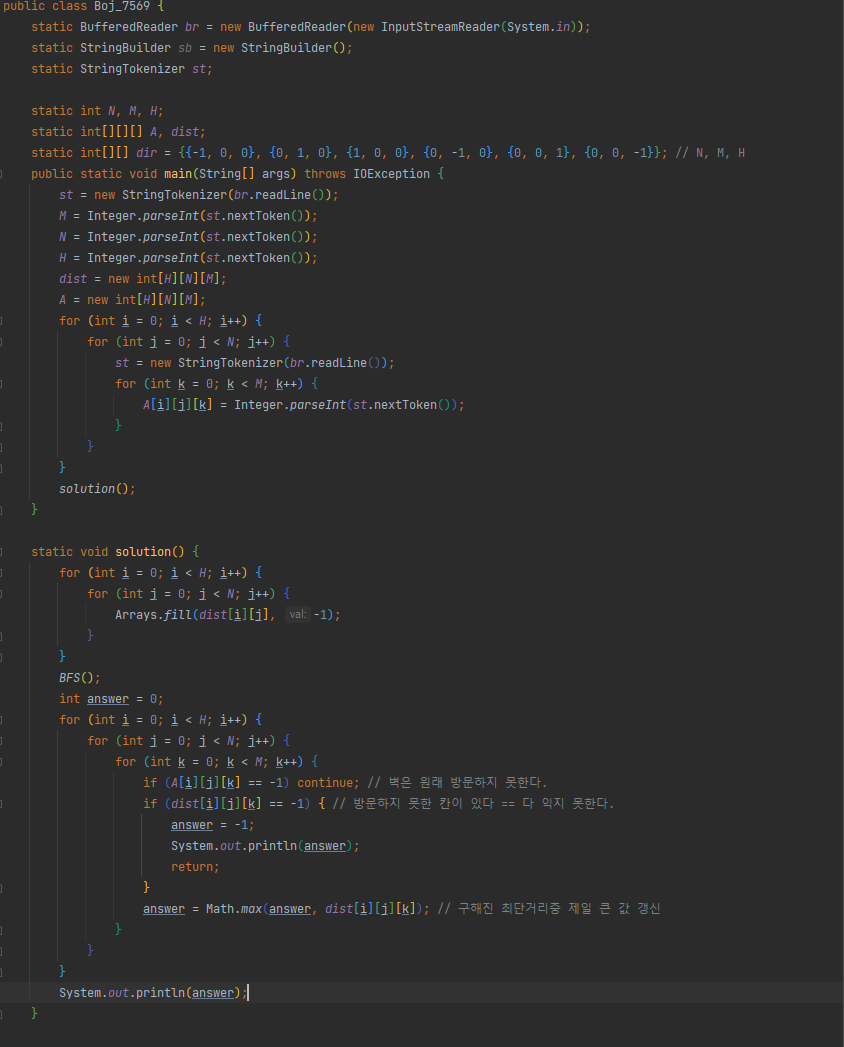
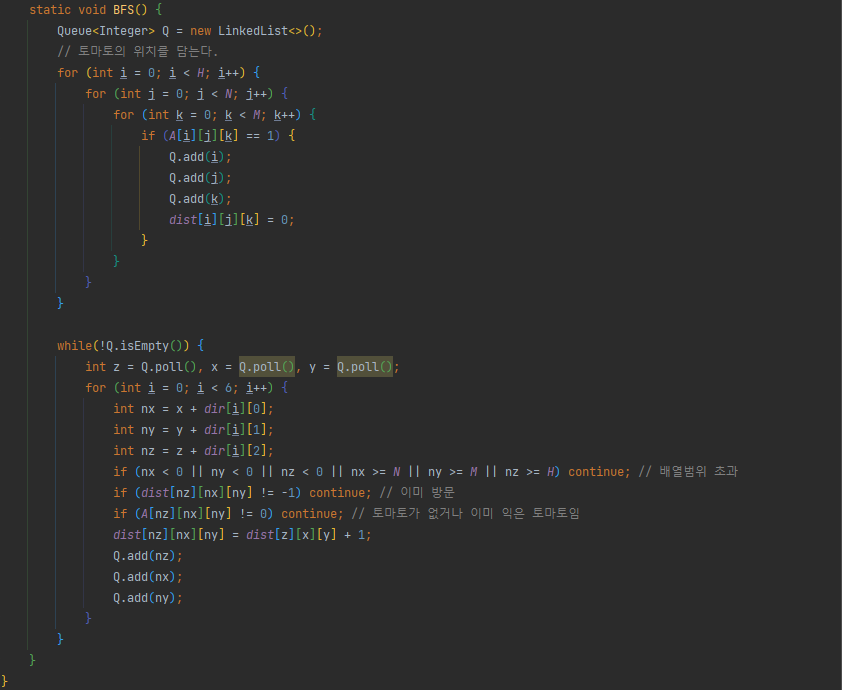
3. 전체코드
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 4803 트리 Java (0) | 2021.12.13 |
|---|---|
| 백준 11725 트리의 부모 찾기 JAVA (0) | 2021.12.13 |
| 백준 3055 탈출 JAVA (0) | 2021.12.09 |
| 백준 5567 결혼식 JAVA (0) | 2021.12.09 |
| 백준 1389 케빈 베이컨의 6단계 법칙 JAVA (0) | 2021.12.08 |