
https://www.acmicpc.net/problem/1240
1240번: 노드사이의 거리
N(2≤N≤1,000)개의 노드로 이루어진 트리가 주어지고 M(M≤1,000)개의 두 노드 쌍을 입력받을 때 두 노드 사이의 거리를 출력하라.
www.acmicpc.net
1. 접근
가장 기본적인 탐색이 각 노드마다의 거리를 누적하여 x ~ y까지 몇 번 이동해야 하는가? 를 물었다면
이번엔 각 간선마다 비용이 있어 그 비용을 누적하면 되는 문제다!
DFS를 활용하여 각 정점까지의 거리를 누적하는 방법과
다익스트라 알고리즘을 활용하는 두 가지의 방법이 있는데
둘 다 구현해보도록 하자!
그림으로 살펴보자!
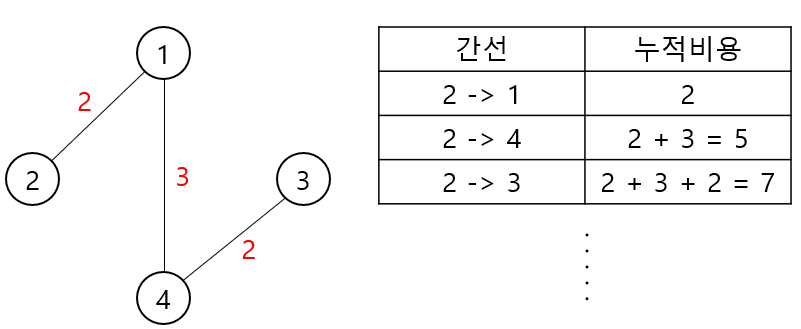
2번 정점에서 출발할 때의 예시이다.
그림 속 표를 글로 쓰면
2번 정점에서 1번 정점까지의 비용 = 2
2번 정점에서 4번 정점까지의 비용 = 5 ( 2 -> 1 -> 4)
2번 정점에서 3번 정점까지의 비용 = 7 ( 2 -> 1 -> 4 -> 3)
이런 식으로 시작 지점부터 각 정점까지의 이동비용을 누적해주고
목적지 정점에 도착했을 때의 비용을 출력해주면 끝이다!
2. 풀이
변수 세팅
static int N, M;
static int[] dist;
static ArrayList<Edge>[] graph;
public static void main(String[] args) throws IOException {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
dist = new int[N + 1];
graph = new ArrayList[N + 1];
for (int i = 1; i <= N; i++) graph[i] = new ArrayList<>();
for (int i = 1; i < N; i++) {
st = new StringTokenizer(br.readLine());
// x좌표 y좌표 이동비용(cost)
int x = Integer.parseInt(st.nextToken()), y = Integer.parseInt(st.nextToken()), c = Integer.parseInt(st.nextToken());
// 무방향 그래프 생성
graph[x].add(new Edge(y, c));
graph[y].add(new Edge(x, c));
}
while (M --> 0) {
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken()), y = Integer.parseInt(st.nextToken());
solution(x, y);
}
}
배열 초기화 및 함수 호출
static void solution(int x, int y) {
//DFS(x, -1, y, 0);
Arrays.fill(dist, Integer.MAX_VALUE); // 비교를 위해 최대값으로 세팅
dijkstra(x, y);
}
DFS 풀이 방법
static void DFS(int x, int prev, int goal, int cost) {
if (x == goal) { // 목적지에 도착했다!
System.out.println(cost);
return;
}
for (Edge edge : graph[x]) {
if (edge.y == prev) continue; // 이전 노드는 방문하지 않는다!
DFS(edge.y, x, goal, cost + edge.c); // 이동 비용 누적
}
}
다익스트라 풀이 방법
static void dijkstra(int x, int y) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.offer(new Edge(x, 0));
dist[x] = 0;
while (!pq.isEmpty()) {
Edge tmp = pq.poll();
int now = tmp.y; // 정점번호
int nowCost = tmp.c; // now로 이동시의 비용
if (nowCost > dist[now]) continue; // 이미 계산되어 있는 비용보다 크다면 굳이 볼 필요 없다!
for (Edge edge : graph[now]) {
if (dist[edge.y] > nowCost + edge.c) { // 이미 계산되어 있는 비용보다 더 적은 비용인가?
dist[edge.y] = nowCost + edge.c; // 해당 정점까지의 비용을 기록한다!
pq.offer(new Edge(edge.y, nowCost + edge.c)); // 새로 offer 할 때 비용을 누적하자!
}
}
}
System.out.println(dist[y]);
}
3. 전체 코드


'알고리즘 > 백준' 카테고리의 다른 글
| 백준 1068 트리 Java (0) | 2021.12.22 |
|---|---|
| 백준 9489 사촌 Java (0) | 2021.12.22 |
| 백준 3584 가장 가까운 공통 조상 Java (2) | 2021.12.17 |
| 백준 20364 부동산 다툼 Java (0) | 2021.12.16 |
| 백준 15900 나무 탈출 java (0) | 2021.12.15 |