
https://www.acmicpc.net/problem/1068
1068번: 트리
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다
www.acmicpc.net
1. 접근
일반적인 트리에서는 노드 제거 시 규칙(?)에 따라 자식 노드가 그 자리를 대체하는 방식이지만 문제에선 제거된 노드는 빈 채로 두어 가지 않는다.
즉, 입력 단계에서 루트가 -1로 주어지는 것만 염두에 두고 평소처럼 자식 노드들을 인접 리스트를 생성하되 마지막 입력인 지울 노드만 별도로 받았다가 탐색 전 경로를 끊어버리면 된다.
예제 입력 2번을 그림으로 보자 (1번 노드를 지울 경우)
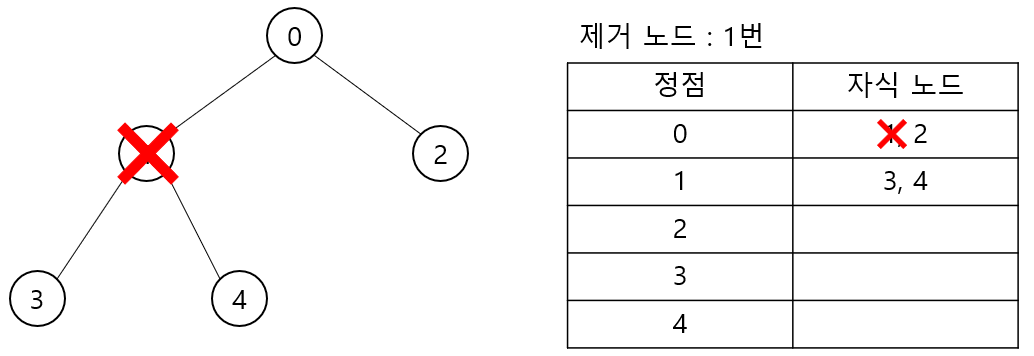
3번 정점과 4번 정점의 경우 이미 0번 정점에서 1번으로 가는 간선 정보를 제거하여 탐색할 수 없다.
그 후 자식 노드가 없는 정점까지 방문하여 부모 정점에 단말 노드의 개수를 차곡차곡 누적 후 루트 노드의 노드 개수를 출력하면 끝이다!
자식 노드를 누적 후 루트에서의 출력은 예제 1번으로 그려보았다.

2. 풀이
변수 세팅
static int N, erase, root;
static ArrayList<Integer>[] graph;
static int[] leaf;
public static void main(String[] args) throws IOException {
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
leaf = new int[N];
graph = new ArrayList[N];
for (int i = 0; i < N; i++) graph[i] = new ArrayList<>();
for (int i = 0; i < N; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent == -1) root = i; // 루트는 부모가 없으니 -1로 주어진다!
else graph[parent].add(i); // 각 노드의 자식들
}
erase = Integer.parseInt(br.readLine()); // 지울 노드
solution();
}
제거 대상 노드 제거 및 탐색
static void solution() {
for (int i = 0; i < N; i++) {
graph[i].removeIf(integer -> integer == erase); // 그래프 안 지울 노드를 삭제하자!
}
if (erase != root) DFS(root, -1); // 루트를 지운다면 탐색할 필요는 없다!
System.out.println(leaf[root]);
}
탐색
static void DFS(int x, int parent) {
if (graph[x].isEmpty()) leaf[x] = 1; // 자식이 없다면 그 노드는 단말 노드다!
for (int y : graph[x]) {
if (y == parent) continue; // 위에서부터 내려왔으니 부모는 볼 필요가 없다!
DFS(y, x);
leaf[x] += leaf[y]; // if문에 의해 1이 누적되었으니 그 값을 부모에 누적하자!
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 14267 회사 문화 1 [JAVA] (0) | 2021.12.27 |
|---|---|
| 백준 15681 트리와 쿼리 [Java] (0) | 2021.12.23 |
| 백준 9489 사촌 Java (0) | 2021.12.22 |
| 백준 1240 노드사이의 거리 Java (2) | 2021.12.20 |
| 백준 3584 가장 가까운 공통 조상 Java (2) | 2021.12.17 |